Entschlüsselung der Musikgeometrie: Lösung eines 70 Jahre alten mathematischen Problems

Einer der Professoren und seine Mitarbeiter bewiesen Polyas Vermutung über die Eigenwerte der Scheibe, ein schwieriges Problem in der Mathematik.

Lässt sich aus den Geräuschen, die sie erzeugt, auf die Form der Trommel schließen?

Das ist die Art von Frage, die Iosif Poltrovic, Professor am Fachbereich Mathematik und Statistik der Universität Montreal, gerne stellt. Poltrovic nutzt die spektroskopische Geometrie, einen Zweig der Mathematik, um physikalische Phänomene bei der Ausbreitung von Wellen zu verstehen.

Ein Durchbruch in der mathematischen Schätzung

Letzten Sommer haben Poltrović und seine internationalen Mitarbeiter – Nikolai Filonov, Michael Levitin und David Scherr – einen Sonderfall der berühmten spektroskopischen Geometrievermutung bewiesen, die 1954 vom bedeutenden ungarisch-amerikanischen Mathematiker George Polya formuliert wurde.

Bei der Schätzung geht es um die Schätzung der Frequenzen des runden Zylinders, oder mathematisch ausgedrückt, der Eigenwerte der Scheibe.

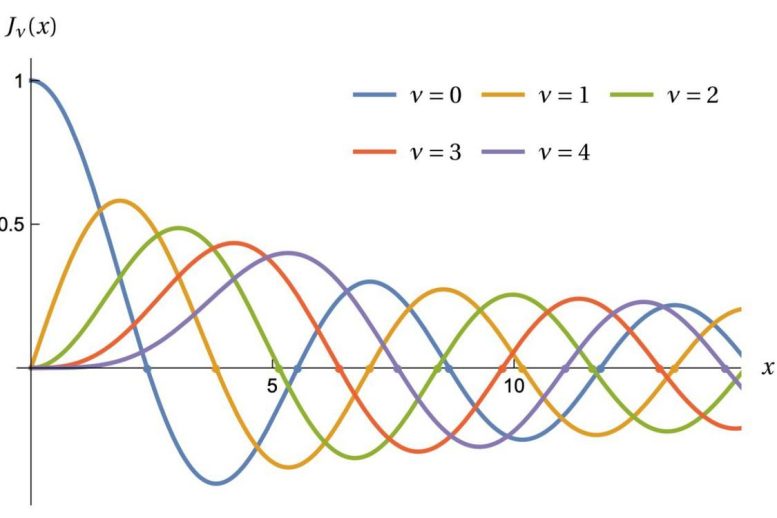
Dieses Diagramm zeigt Bessel-Funktionen, wobei die Punkte den Frequenzen der von einer runden Trommel erzeugten Töne entsprechen. Bildnachweis: Michael Levitin

Polya selbst bestätigte 1961 seine Vermutung über die Kugeln, aus denen die Ebene besteht, wie Dreiecke und Rechtecke. Bis letztes Jahr war die Vermutung nur für diese Fälle bekannt. Trotz ihrer scheinbaren Einfachheit blieb die CD schwer fassbar.

„Stellen Sie sich einen unendlichen Boden vor, der mit Fliesen derselben Form bedeckt ist, die zusammenpassen, um den Raum zu füllen“, sagte Poltrovic. „Sie können mit Quadraten oder Dreiecken gekachelt werden, aber nicht mit Scheiben. Eine Scheibe ist eigentlich keine gute Form für die Tessellation.“

Die Universalität und Wirkung der Mathematik

In einem im Juli 2023 im Sportmagazin veröffentlichten Artikel Erfindungen der MathematikDie Forscher zeigten, dass Bolyas Vermutung für eine Scheibe zutrifft, ein Fall, der als besonders schwierig gilt.

Obwohl ihre Ergebnisse hauptsächlich theoretischen Wert haben, findet ihre Beweismethode Anwendung in der Computermathematik und im numerischen Rechnen. Die Autoren untersuchen nun diesen Ansatz.

Joseph Poltrovic

„Obwohl Mathematik eine Grundlagenwissenschaft ist, ähnelt sie in mancher Hinsicht dem Sport und den Künsten“, sagte Poltrovic.

„Der Versuch, eine langjährige Vermutung zu beweisen, ist ein Sport. Eine elegante Lösung zu finden ist eine Kunst. In vielen Fällen sind schöne mathematische Entdeckungen nützlich, man muss nur die richtige Anwendung finden.“

Referenz: „Die Polya-Vermutung für euklidische Sphären“ von Nikolai Filonov, Michael Levitin, Iosif Poltrovic und David A. Teilen, 5. Juni 2023, Mathematische Erfindungen.
doi: 10.1007/s00222-023-01198-1